1. 진실과 판단의 4패턴
- 가설검정 : 귀무가설 & 대립가설을 고려 (서로 대립 관계x, 부정 관계o)
- 진실 : 2가지 패턴
(i) 귀무가설(참) & 대립가설(거짓)
(ii) 귀무가설(거짓) & 대립가설(참)
- 판단 : 2가지 패턴 at 가설검정, p값 계산 → 유의수준 𝝰와 비교 ⇒ 대립가설을 지지할지, 판단을 보류할지 결정
(i) p < 𝝰 : 귀무가설을 기각 & 대립가설을 채택
(ii) p ≥ 𝝰 : 귀무가설을 기각할 수 x
- 진실과 판단은 2x2 패턴

- 왼쪽 위 칸 : 귀무가설 "참" → 귀무가설을 기각하지x (O)
- 오른쪽 아래 칸 : 대립가설 "참" → 대립가설 채택 (O)
- 왼쪽 아래 칸 : 귀무가설 "참" → 귀무가설 기각, 대립가설 채택 (X) "제1종 오류(일어날 확률 𝝰)"
- 오른쪽 위 칸 : 대립가설 "참" → 귀무가설을 기각하지x (X) "제2종 오류(일어날 확률 𝝱)"
1) 제1종 오류 type 1 error (= 위양성 false positive)
- at 평균값 비교, 제1종 오류 : 실제로는 아무런 차이가 없는데도, 차이가 있다고 판단해 버림 "약의 효과가 없는데도 있다고 판단"
- [BUT] 우리는 진실(모집단)을 알 수 x, 해석 결과가 제1종 오류를 범했는지 알 수 x → 대신, p값 & 유의수준 𝝰 를 이용; 제1종 오류가 일어날 확률을 통제할 수o
- p값 : 귀무가설이 옳다고 가정했을 때, 실제로 얻은 데이터 이상으로 극단적인 값이 나타날 확률 → 확보한 데이터가 정말로 귀무가설에서 얻은 것이라면, p<𝝰 일 확률은 𝝰 ∴ 𝝰를 경계로 귀무가설을 기각하면, 귀무가설이 옳은데도 착오로 귀무가설을 기각해버리는 오류가 확률 𝝰로 발생
- 즉, 유의수준 𝝰의 값을 미리 정해둠으로써, 제1종 오류가 일어날 확률을 통제할 수o
[EX] 𝝰 = 0.05
- 정의 : 귀무가설이 옳을 때, 평균적으로 20번 중 1번은 귀무가설을 착오로 기각 & 대립가설을 채택한다는 뜻
- 이 조건에서, 전혀 효과가 없는 약을 20종류 준비 → 각 약의 효과를 검증 → 평균 1종류의 약에는 통계적으로 유의미한 차이가 나타나 약 효과가 있다고 주장하게 됨 "이러한 잘못이 20번 중 1번 정도 일어나는 위험을 허용한단 뜻"
2) 제2종 오류 type 2 error (= 위음성 false negative)
- 제2종 오류 : 실제로 차이가 있는데도 차이가 있다고는 말할 수 없어, 귀무가설을 기각하지 않는 판단을 해버림 "약의 효과가 있는데(𝜇ᴬ - 𝜇ᴮ ≠ 0), 효과가 있다고 말할 수 없다 판단"
- 𝝱 : 제2종 오류가 발생하는 확률
- 표본크기 n이 커질수록 작아짐
- 효과크기(어느 정도의 차이를 차이로 간주하는지 나타내는 값)가 커질수록 작아짐
- 1-𝝱 (검정력 power of test) : 제2종 오류가 발생하지 않는 확률 "실제로 차이가 있을 때, 차이가 있다고 올바르게 판단할 확률"
- 표본크기 n이 커질수록 커짐
- 일반적으로 1-𝝱 을 80%로 설정 [BUT] 𝝱, 1-𝝱 는 𝝰와 달리 직접 통제할 수 x → 표본크기, 효과크기와의 관계를 통해 1-𝝱 이 80%가 되도록 표본크기를 설계 "이상적인 가설검정의 순서"
2. 𝝰, 𝝱 는 상충 관계
- 제1종 오류 & 제2종 오류가 발생할 확률 𝝰, 𝝱를 모두 0에 가깝게 만들고 싶음 [BUT] 𝝰, 𝝱 는 서로 상충 관계; 한쪽이 작아지면 또 다른 한쪽은 커짐
- 𝝰, 𝝱의 관계 : 표본크기 n에 따라 달라짐 표본크기 n이 클수록 검정력 1-𝝱 가 상승함 *검정력 : 실제로 차이가 있을 때, 그렇다고 판단할 확률

[EX] 이표본 t검정에서의 𝝰, 𝝱 관계를 시각화한 그림 (각 표본's 모집단 표준편차 = 1, 평균값의 차이 = 1 로 설정)
- 자주 사용되는 𝝰 = 0.05 를 𝝰 = 0.01로 변경하면, 제1종 오류가 발생할 확률 𝝰 를 5%에서 1%로 줄일 수 있음 BUT, 제2종 오류가 발생할 확률 𝝱 가 증가하게 됨
- 표본크기 n이 커지면, 왼쪽 아래로 곡선이 이동; 𝝰 값 고정시, n이 커짐에 따라 𝝱가 줄어듦
3. 효과크기를 달리 했을 때의 𝝰, 𝝱
- 효과크기 (d, effect size) : 얼마나 큰 효과가 있는지를 나타내는 지표
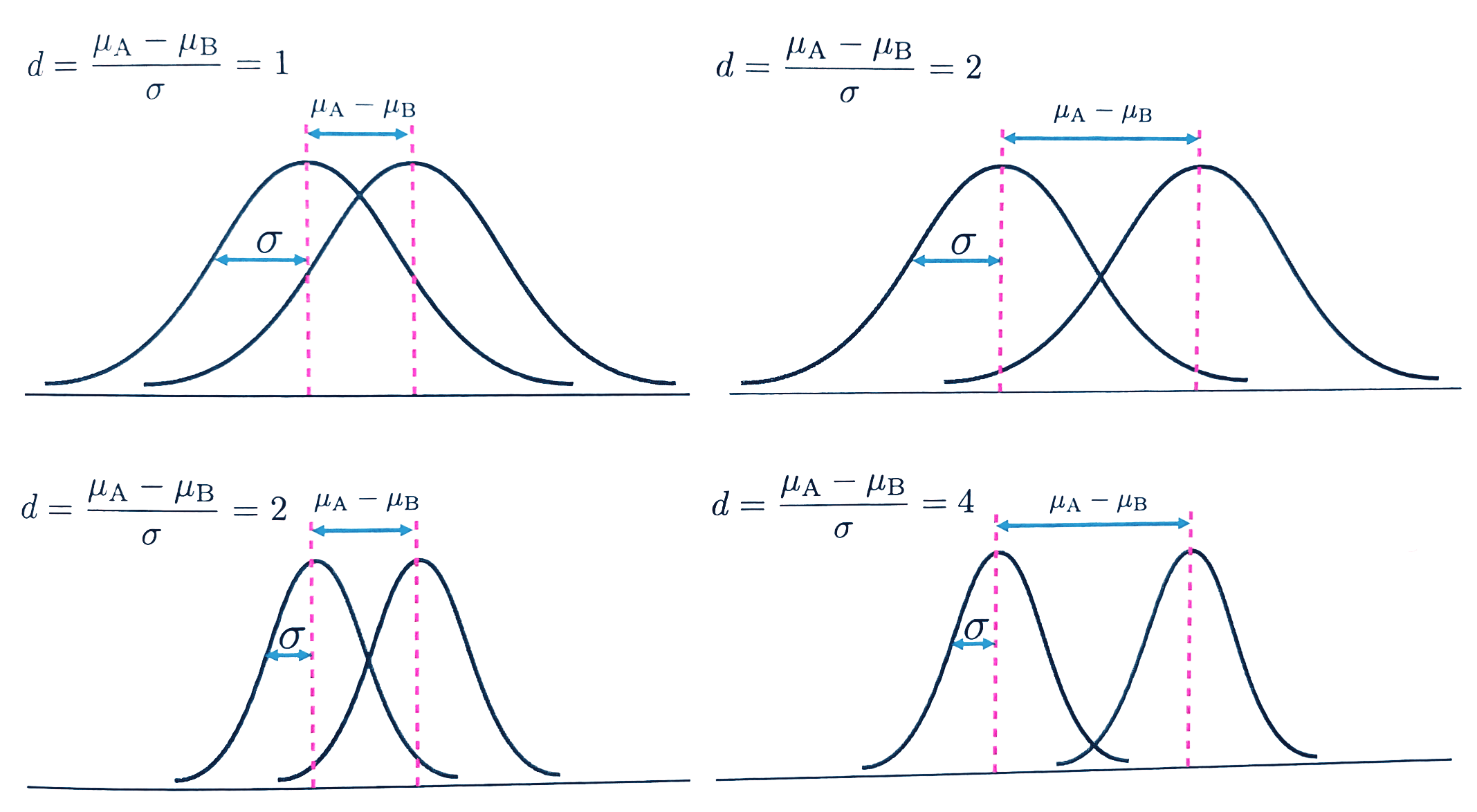
[EX] 2개 집단의 표준편차가 같다고 가정하여 단순화된 그래프로 나타냄 *𝜇ᴬ - 𝜇ᴮ : 모집단 A, B의 평균값 차이, 𝝈 : 모집단 A, B 각각의 표준편차
- 왼쪽 위 : (𝜇ᴬ - 𝜇ᴮ) ・ 𝝈 가 서로 비슷한 값일 경우
- 오른쪽 위 : 𝝈는 그대로, (𝜇ᴬ - 𝜇ᴮ)는 2배 큰 값일 경우
- 아래쪽 두 그래프 : 위쪽과 마찬가지이나, 𝝈를 절반으로 줄임
- 2개 집단의 평균값; 원래 갖고 있는 모집단's 데이터 퍼짐에 대해 상대적으로 평가한 값 d = (𝜇ᴬ - 𝜇ᴮ)/𝝈 를 사용 단순히 평균값의 절대적인 차이에만 주목x
- (𝜇ᴬ - 𝜇ᴮ)에 비해, 원래 퍼짐 정도인 𝝈가 ↑수록 2개 분포의 겹치는 부분↑; 효과크기 d↓ & (𝜇ᴬ - 𝜇ᴮ)는 검출하기 어려워짐
- (𝜇ᴬ - 𝜇ᴮ)에 비해, 원래 퍼짐 정도인 𝝈가 ↓수록 2개 분포의 겹치는 부분↓; 효과크기 d↑
- at 가설검정, 모집단을 대상으로 검출하고 싶은 효과크기를 미리 설정하는 것이 바람직
[EX] 혈압을 내리는 약의 효과를 검증할 때
- 무작정 표본크기 n이 아주 큰 실험을 진행, 평균 혈압 하락이 0.1mmHg인 극히 작은 효과를 검출 → 이는 혈압약으로써 의미가 있는 효과가 x
- 이러한 문제를 피하기 위해 검출하고자 하는 효과를 미리 설정하고 실험을 진행해야 함
- 𝝰, 𝝱, n, d 의 네 값 중 셋을 결정 → 나머지 하나는 자동으로 정해짐; 𝝰 = 0.05, 1-𝝱 = 0.8, 검출하고자 하는 효과크기 d를 미리 설정 → 가설검정에 필요한 표본크기 n을 구할 수 o

- 효과크기 d가 ↑수록 𝝱↓ ∵d가 ↑수록 분포가 겹치는 부분이↓; 검출이 간단해짐
출처 : ⎡통계101 x 데이터 분석 (아베 마사토)⎦
'통계학 > 05. 가설검정' 카테고리의 다른 글
| 05-3 가설검정 관련 그래프 (1) | 2024.07.05 |
|---|---|
| 05-2 가설검정 시행 (1) | 2024.07.05 |
| 05-1 가설검정의 원리 (0) | 2024.07.05 |


