📖 신뢰구간이란?
표본오차의 확률분포를 통해, 얼마나 큰 오차가 어느 정도의 확률로 나타나는지 확인
→ 이 때 오차를 정량화하기 위해, 신뢰구간(confidence interval) 개념 도입
- at 표준정규분포, (𝜇 - 2𝝈) ~ (𝜇 + 2𝝈) 범위에 약 95%의 값이 포함됨; 표준정규분포에서 하나의 값을 무작위로 꺼내면 약 95%의 확률로 그 범위에 포함된다는 뜻
- 표본오차(x̅ - 𝜇)의 정규분포; 노란색・초록색 박스가 95% 신뢰구간

1. 신뢰구간 개념 알기
1) 신뢰구간의 해석
- '○○% 신뢰구간' : "○○%의 확률로 이 구간에 모집단평균 𝜇가 존재"
- 이 때, 확률변수는 표본평균 x̅(or 신뢰구간) 모집단평균 𝜇가 x
- 모집단에서 표본을 추출하여 ○○% 신뢰구간을 구하는 작업을 100번 반복했을 때, 평균적으로 그 구간에 𝜇가 포함되는 것이 ○○번 발생 𝜇가 확률적으로 변화하여 그 구간에 포한되는 것이 x
- 하나의 표본에서 얻은 신뢰구간은 𝜇를 포함하거나 ・ 포함하지 않거나 둘 중 하나
- 신뢰구간 : 표본에서 구한 모집단 𝜇의 추정값을 어느정도 신뢰할 수 있는지를 나타냄
- 신뢰구간이 좁음 : 추정값 가까이에 𝜇가 존재; 추정값은 신뢰할 수 있는 값
- 신뢰구간이 넓음 : 추정값 ~ 모집단평균𝜇 사이의 오차가 커짐. 신뢰도가 낮음
- 일반적으로 95%의 신뢰구간을 사용 = 유의수준 5%
2) 신뢰구간의 예
- 모집단 평균이 신뢰구간에 포함될 때의 예 : 키(cm) 표본

- 표본크기 n=10 → 표본평균(x̅), 표준편차(s), 표준오차(s / √n) 구할 수 o
- 정규분포의 성질, 모집단평균 𝜇은 {(x̅ - 2 x s/√n) ≤ 𝜇 ≤ (x̅ + 2 x s/√n)} 구간에 약 95% 확률로 존재
- 모집단 평균이 신뢰구간에 벗어날 때의 예 :

- 𝜇=170인 모집단에서 표본크기 n=10인 표본을 추출, 95% 신뢰구간을 그리는 작업을 20번 반복
- 18번째 표본으로 그린 95% 신뢰구간 : 모집단평균 𝜇(파란색 선)를 포함하지 x
- 즉, 95% 신뢰구간 : 평균적으로 20번 중 1번 정도 벗어난다는 뜻(= 20번 중 19번은 구간에 모집단평균을 포함함)
2. t분포와 95% 신뢰구간
- 95% 신뢰구간
- 대략적 의미 : "표본평균±2 * 표준편차" 안에 약 95%의 확률로 모집단 평균이 존재
- 정확한 의미 : "표본평균±1.96 * 표준편차" 안에 95%의 확률로 모집단 평균이 존재
- 중심극한정리 : 표본평균x̅의 분포를 히스토그램으로 나타냈을 때, 표본크기 n이 커질수록 x̅의 분포가 정규분포(𝜇, 𝝈 / √n)에 근사함
- BUT 실제 데이터 분석에서, 작은 표본크기의 경우 표본오차가 정규분포를 따른다고 말할 수 x
- 모집단의 𝝈 대신 s 를 사용
⇒ 이 때 사용하는 것이 t분포; 작은 표본으로 모집단 전체를 추정
1) t 분포
- t분포 : 모집단=정규분포 라는 가정하에, 𝝈를 s로 대응했을 때, 표본오차(x̅ - 𝜇)를 표준오차(s / √n)로 나누어 표준화한 값이 따르는 분포 * 𝝈 = 미지의 모집단 표준편차, s = 표본으로 계산한 비편향표준편차 **표본평균x̅으로 정규분포를 그린 뒤, 표준화한 변수Z가 따르는 분포
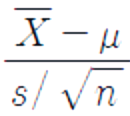
- t분포는 정규분포와 매우 비슷한 형태

- 표본크기 n에 따라 모양이 조금씩 달라짐
- 표본크기 n이 커짐에 따라, t분포는 정규분포에 가까워짐
- 하위 2.5%나 상위 2.5% 지점은 가운데 95% 영역과 그 외 영역의 경계점을 나타냄
- at 정규분포(평균0, 표준편차1), -1.96 ・ +1.96
- at t 분포(표본크기 n=10), -2.26 ・ +2.26
- ∴ t 분포의 신뢰구간을 구하는 식 ; "표본평균±2.26 * 표준오차(s / √n)"으로 95% 신뢰구간을 구함
2) 정밀도를 높이려면
- 보다 신뢰할 수 있는 평균값을 추정하려면 표준오차(s / √n)에 주목! *표준오차 : 오차분포의 너비
- 표준오차를 작게 만들기 위한 방법
(i) 분자 '비편향표준편차 s'를 작게하기
- s(or 𝝈) : 모집단 데이터 퍼짐(모집단 그 자체의 성질)에서 유래. 작게만들기 어려움
- BUT 측정한 데이터 퍼짐 정도를 줄일 수는 있음 by 측정을 더 정밀하게~
(ii) 분모 '표본크기 n'을 크게하기
- n을 크게 만듦으로써 더 높은 정밀도로 추정
- 표준오차의 분모는 √n 이므로, 신뢰구간을 1/a 로 좁히고 싶다면 표본크기 n을 a²배로 늘려야 함
- 𝝈와 n에 따른 신뢰구간의 크기
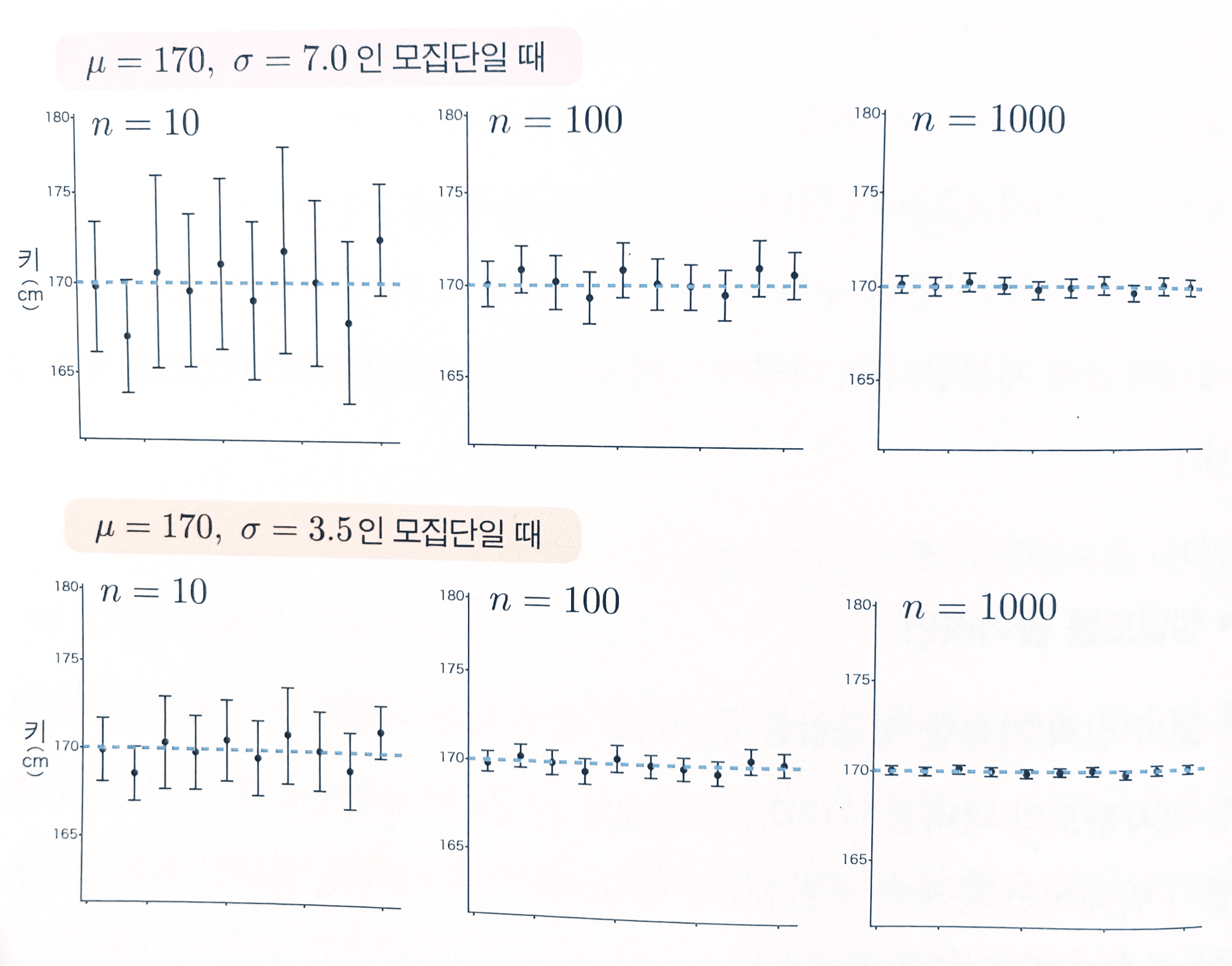
- 𝝈를 적게 하거나 n을 크게 함으로써 표본평균x̅이 얼마나 모집단평균𝜇에 가까운 값을 갖는지・신뢰구간이 얼마나 짧아지는지 알 수 o
3) t 분포 사용시 주의할 점
- 표본크기n이 작아도 적용 가능한 t 분포 : '정규분포(모집단)에서 얻은 데이터'라는 가정이 필요
- 즉, t 분포는 데이터 x₁, x₂, ..., xₙ을 정규분포 모형에서 얻었을 때의 표준화된 표본오차가 따르는 분포
- 데이터의 배경이 되는 모집단분포가 완벽한 정규분포일 수는 x, ∴ 얻은 95% 신뢰구간은 정확한 95%가 아님
- 정규분포와 현저하게 다른 모집단에서 데이터를 얻었을 경우 95% 신뢰구간을 구해도 95%에서 벗어날 수 있어 주의를 요함
- 단, 표본크기n이 클 때, 중심극한정리에 의해 모집단이 정규분포가 아니더라도 표본평균을 정규분포로 근사할 수 있음; 신뢰구간이 정확해짐
3. 신뢰구간과 가설검정
- 가설검정 : 또 하나의 추론통계 방법(like 신뢰구간)
- 가설검정은 신뢰구간을 구하는 것과 동전의 양면 관계
출처 : ⎡통계101 x 데이터 분석 (아베 마사토)⎦
'통계학 > 04. 추론통계~신뢰구간' 카테고리의 다른 글
| 중간점검) 표준편차, 표본오차, 표준오차 용어 정리 (0) | 2024.07.04 |
|---|---|
| 04-2 표본오차 (0) | 2024.06.11 |
| 04-1 추론통계를 배우기 전에... (2) | 2024.06.11 |

