1. 배경 이론
1) 내 필기..

2) 용어 정리
- 확률변수 X : 어떤 사건・현상을 실수로 전환하는 함수
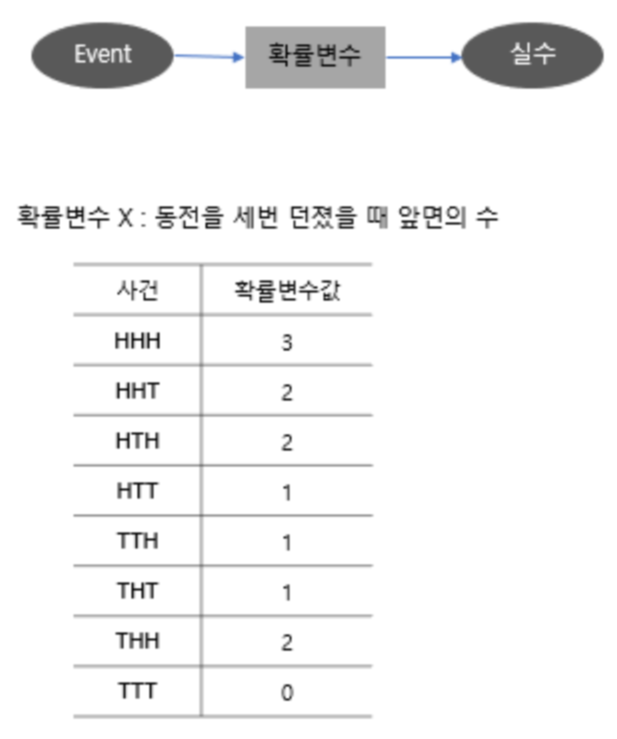
- 확률분포 : 각각의 확률변수 값이 나타날 확률의 분포를 나타낸 것
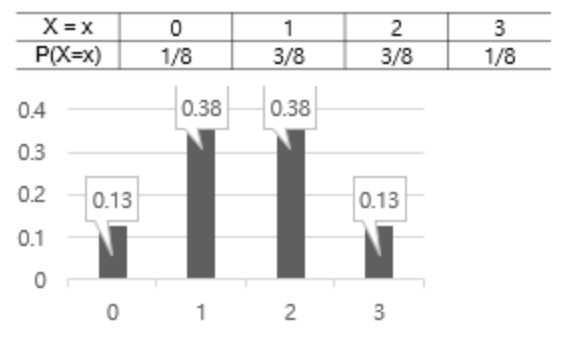
- 확률분포 ⊃ 이산형 확률분포, 연속형 확률분포
- 이산형 확률분포 ⊃ 이항분포, 포아손분포, 기하분포, 초기하분포 등
- 연속형 확률분포 ⊃ 정규분포, f 분포, t 분포, chi-square 분포 등
- 정규분포 : 평균을 중심으로 좌우대칭인 연속형 확률변수's 확률분포 X~N(𝜇, 𝝈²) : 확률변수X(평균𝜇, 분산𝝈²)의 정규분포
- 중심극한정리 : 표본크기 n이 일정 이상 크다면 모집단의 분포가 무엇이든 간에 표본평균x̅의 분포는 정규분포(평균𝜇, 표준편차𝝈/√n)를 따름
- 표준정규분포 : 확률변수Z = (X-𝜇)/𝝈 Z~N(0, 1) : 확률변수Z(평균0, 분산1)의 표준정규분포
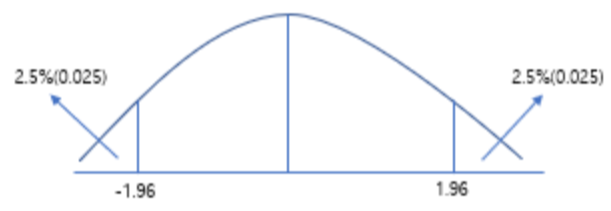
- 표준정규분포의 확률변수 Z가 -1.96 ~ +1.96 사이에 있을 확률 : 95%
= 모집단평균𝜇이 x̅ ± (1.96 x 𝝈/√n) 사이에 있을 확률 : 95%
*𝝈/√n : 표본평균x̅의 표준편차 = 표준오차
3) 표준편차, 표본오차, 표준오차 이해하기
- 표준편차 SD; Standard Deviation
- 정의 : at 정규분포, 분산의 제곱근. 평균을 중심으로 그래프의 퍼짐 정도를 표현 "표본조사로 얻은 각 관측값과 표본평균의 차이"
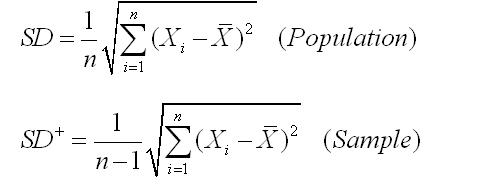
- 표본오차 Sampling Error
- 정의 : 표본평균x̅으로부터 모집단평균𝜇을 추정할 때, 허용할 수 있는 최대한의 오차 "표본을 뽑을 때 모집단을 온전히 대표한다 말할 수 있는 표본을 뽑는걸 실패하는 데에서 발생하는 오차"
- x̅-𝜇
- 표준오차 SE; Standard Error
- 정의 : 표본평균x̅으로부터 모집단평균𝜇을 추정할 때, 발생할 수 있는 오류의 크기 "오차분포의 너비"
- 표본크기 n이 일정 이상 클 때(중심극한정리), 확률변수x̅를 가로축으로 한 정규분포's 표준편차 𝝈/√n = 확률변수x의 표준오차
⇒ 이 때, n이 일정 이상 크지 않거나(t분포) 𝝈가 알려져 있지 않다면 표준오차는 s/√n 이 됨
'통계학 > 04. 추론통계~신뢰구간' 카테고리의 다른 글
| 04-3 신뢰구간 (0) | 2024.07.04 |
|---|---|
| 04-2 표본오차 (0) | 2024.06.11 |
| 04-1 추론통계를 배우기 전에... (2) | 2024.06.11 |

