1. 확률이란?
1) 확률
- 확률 : 발생 여부가 불확실한 사건의 발생 가능성을 숫자로 표현한 것
- 사건 A의 확률 P(A) ex : P(X=붉은 구슬) = 4/5, P(X=흰 구슬) = 1/5
- 0 ≤ P(실수) ≤ 1 ; 큰 값일 수록 발생하기 쉬움
- 모든 사건의 확률을 전부 더하면 1이 됨
2) 확률변수
- 확률변수 : 확률이 달라지는 변수 ex : X = {붉은 구슬, 흰 구슬}
- 실현값 : 확률변수가 실제로 취하는 값 ex : X = 붉은 구슬, 흰 구슬
3) 확률분포
- 확률분포 : '가로축 - 확률변수', '세로축 - 그 확률변수의 발생 가능성'을 표시한 분포
(i) 확률변수 = 이산형 양적 변수
(ii) 확률변수 = 연속형 양적 변수
- 값에 일정한 범위를 두고 확률을 구함; 이 때 확률을 계산하는 함수 '확률밀도함수'
- 확률밀도함수 : '가로축 - 확률변수', '세로축 - 상대적인 발생가능성(그 자체의 값x)
- 확률변수가 어떤 값에서 어떤 값까지의 범위에 들어갈 확률을 알고 싶을 때
: 확률밀도함수를 적분 → x축 & 확률밀도함수로 둘러싸인 부분의 넓이('확률')를 구함
- 확률변수의 정의역 전체를 적분하면 '1'; 모든 사건 중 어느 것이든 일어날 확률이 '1'
4) 추론통계와 확률분포
다음과 같이 가정함으로써, 다루기 어려운 '모집단·표본 데이터'을 '확률분포·실현값'으로 치환
- 현실 세계's 모집단 → 수학 세계's 확룰분포
- 표본 데이터 → 그 확률분포에서 생성된 실현값
* 통계적 추론 : 얻은 데이터로부터 그 발생원이 어떤 확률분포를 취하는지 추정하는 것
* 실현값 : 확률변수가 실제로 취하는 값
5) 기댓값(expected value, E(X))
- 기댓값 : 어떤 확률을 가진 사건을 무한히 반복했을 경우 얻을 수 있는 값의 평균으로써 기대할 수 있는 값
- 확률변수 X의 기댓값 E(X)
- 기댓값을 아주 단순하게 얘기하면 '평균(average)'이라고 할 수 있음
- 기댓값을 구해야하는 이유 : 주사위를 한 번 던져 나온 값이 주사위를 던졌을 때 나오는 일반적인 값이라 할 수 없음. 따라서 여러번 시행하여 그에 대한 평균으로 비교해야 함(주사위를 던졌을 때의 기대할 수 있는 값은 3.5, 즉 평균적으로 3.5 정도를 기대할 수 있음)
① 이산형
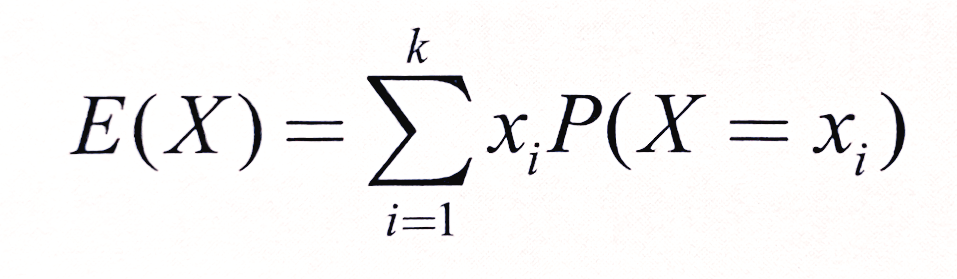
- k : 확률변수가 가질 수 있는 실현값의 개수
- 확률변수가 이산형일 때 기댓값 E(X) : 각 실현값과 그 값이 발생할 확률을 곱하여 더함
ex : at 주사위, 실현값은 xᵢ={1, 2, 3, 4, 5, 6}이고, 확률 P(X=xᵢ)는 모든 xᵢ가 1/6 이므로, 기댓값은 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = 3.5
② 연속형

- 확률변수가 연속형일 때 기댓값 E(X) : 실현값 x와 그에 대응하는 확률밀도 f(x)를 곱한 후, 적분한 값
- 적분 범위 : 확률변수가 정의된 전 범위
6) 분산과 표준편차
- 분산 : 확률분포가 기댓값 주변에 어느 정도 퍼졌는지를 나타내는 값
- 확률변수 X의 분산 V(X)
- 표준편차 : 분산 V(X)에 제곱근을 취한 값
[TIP] 분산・표준편차의 성질
- 0 이상
- 모두 같은 값이 나타나는 경우엔 '0'
- 기댓값에서 떨어진 값이 많을수록 커짐
① 이산형

② 연속형

- 두 식 모두 기댓값과의 차이를 제곱한 값을 통해 데이터가 기댓값에서 어느 정도 떨어져 있는지를 평가함
7) 왜도와 첨도
- 왜도(skewness) : 분포가 좌우대칭에서 어느 정도 벗어났는지
- 첨도(kurtosis) : 분포가 얼마나 뾰족한지・그래프의 꼬리가 차지하는 비율이 얼마인지(분포의 양쪽 끝 꼬리의 확률 크기)
2. 확률변수가 2개일 때
확률변수가 여러 개라면 그 사이의 관계성을 생각할 수 있음
1) 동시확률분포 P(X, Y)
- 동시확률분포 : 확률변수 2개를 동시에 생각할 때의 확률분포
- ex : 2개의 주사위 A, B → A에서 나온 눈을 X, B에서 나온 눈을 Y; A가 1의 눈이 나오는 동시에 B가 2의 눈이 나올 확률 P(X=1, Y=2)
① 독립
- 'X, Y 2개 확률변수가 독립' = 'X와 Y의 동시확률분포 P(X, Y)가 각각의 확률 P(X)와 P(Y)의 곱과 값음'

- 한쪽이 어떤 값을 취하든지, 다른 한쪽의 발생 확률은 변하지 않음
2) 조건부확률 P(X|Y)
- 조건부확률 : 확률변수 Y를 알 때, 다른 한쪽 확률변수 X의 확률
- '|' 를 기준으로 오른쪽 - '조건', 왼쪽 - '확률변수'
- 이는 곧 Y의 정보를 얻으면 X를 알 수 있다는 뜻 이와 달리, X와 Y가 독립인 경우 P(X|Y) = P(X) 'Y가 어떤 값이 되든 X가 발생할 확률은 변하지x'
출처 : ⎡통계101 x 데이터 분석 (아베 마사토)⎦
'통계학 > 03. 통계분석의 기초' 카테고리의 다른 글
| 03-4 이론적인 확률분포 (0) | 2024.06.11 |
|---|---|
| 03-2 통계량 (0) | 2024.06.10 |
| 03-1 데이터 유형・분포 (0) | 2024.06.09 |

