1. 데이터 특징 짓기
1) 히스토그램 : 대략의 데이터 분포를 시각적으로 살펴봄 BUT 데이터를 객관적·정량적으로 평가 불가
→ 데이터를 수치로 변환하여 특징 짓는 방법이 필요
2) 통계량 : 수집한 데이터로 이런저런 계산을 수행하여 얻은 값
→ 데이터 분석 : 다양한 통계량 계산을 통해 대상을 이해하는 과정
3) 기술통계량(= 요약통계량) : 데이터 그 자체의 성질을 기술·요약하는 통계량
→ 데이터에서 몇 가지 통계량을 계산·요약하면 데이터가 어떻게 분포하는지 정량적으로 특징지을 수 있음(like 히스토그램)
- 기술통계량은 주로 수치형 변수를 대상으로 계산(범주형 변수인 경우 '특정 범주의 값이 몇 개인지' 같은 개수(or 비율)로만 데이터를 기술·요약할 수 있음)
- ex : 평균값; raw data의 수많은 요소들을 평균값이라는 하나의 값으로 요약 → 대략 어떤 분포인지 특징지을 수 있음
2. 다양한 기술통계량
1) 대표적인 기술통계량
기술통계량에는,
- 대략적인 분포 위치를 나타내는 대표값인 평균값, 중앙값, 최빈값이 있음
- 데이터 퍼짐 정도를 나타내는 분산, 표준편차가 있음
2) 대표값
- 대표값(representative value) : 대략적인 분포 위치(대표적인 값)를 정량화하기 위해 사용하는 통계량 '분포가 어느 부근에 있는지'
- 대표값에는 평균값, 중앙값, 최빈값이 있음
- 대표값으로 집약시 사라지는 정보도 있으므로(ex : '데이터가 어느 정도로 분포되어있는지' / '데이터에 포함된 최대값·최소값이 얼마인지' 는 대표값에서 읽을 수 x) 다른 통계량도 함께 확인하는 것이 중요
"처음엔 히스토그램으로 대략적 파악 → 대표값으로 적절하게 분포를 특징지을 수 있는지 확인"
① 평균값 (mean, =표본평균)

② 중앙값 (median) : 크기 순으로 값을 정렬했을 때 한가운데 위치한 값
- 중앙값은 수치 자체의 정보가 아닌, 순서에만 주목하므로 극단적으로 크거나 작은 값이 있어도 영향을 받지 않음
③ 최빈값 (mode) : 데이터 중 가장 자주 나타나는 값
- 연속변수일 경우 일정 범위를 정한 뒤, 그 사이에 들어가는 데이터 개수로 정함(like 히스토그램)
3) 대표값의 모습
(i) 좌우대칭에 가까운 봉우리 형태 분포
→ 평균값, 중앙값, 최빈값이 거의 일치
(ii) 좌우 비대칭 분포
→ 평균값, 중앙값, 최빈값이 불일치
4) 이상값이 대표값에 미치는 영향
- 극단적으로 큰·작은 값인 이상값(outlier)이 데이터에 포함될 경우가 있음
- 평균값 : 계산시 모든 값을 고려하므로 이상값 영향↑
- 중앙값 : 가운데 있는 값만 참조하므로 이상값 영향↓
- 최빈값 : 이상값의 빈도가 낮으므로 영향x
5) 분산과 표준편차
- 데이터 퍼짐을 평가하기 위해서는 분산(=표본분산)·표준편차(=표본표준편차) 통계량을 계산
- 분포의 넓이가 넓어질수록, 분산·표준편차가 커짐
① 분산 (variance) : 표본의 각 값과 표본평균이 어느 정도 떨어져 있는지를 평가함. 데이터 퍼짐 상태를 정량화한 통계량

[TIP] 분산의 성질
- s² ≥ 0
- 모든 값이 같다면 0
- 데이터 퍼짐 정도가 크면 s²이 커짐
② 표준편차 (standard deviation, S.D.) : 분산에 제곱근을 취한 값

[TIP] 분산 vs 표준편차
분산's 단위 : 원래 값 단위의 제곱
표준편차's 단위 : 원래 값 단위와 일치
→ 데이터 퍼짐 정도를 정량화된 지표로 나타낼 때, 표준편차가 더 알기 쉬움
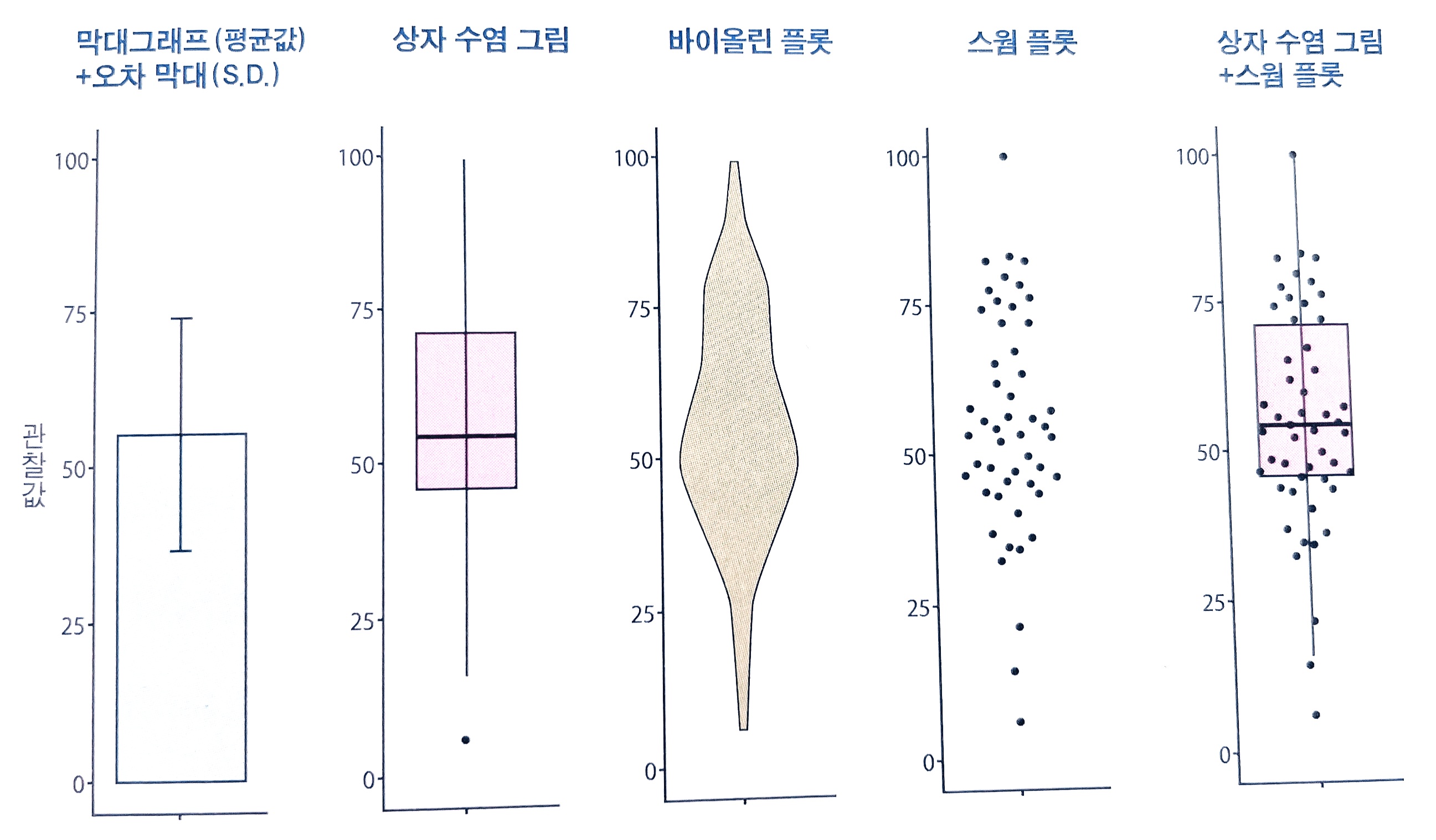
6) 분포를 시각화하는 다양한 방법
데이터 분포를 시각화하기 위한 수단 : 히스토그램, 상자 수염 그림,...
① 상자 수염 그림(box-and-whisker plot)
- 상자&수염으로 구성; 사분위수·중앙값이라는 통계량을 나타냄으로써 데이터의 분포를 눈으로 확인
- 중앙값·사분위수·최댓값·최솟값의 통계량은 나타내는 반면, 히스토그램의 상세한 분포 형태는 포함x
- 상자 : 제1사분위~제3사분위 까지의 범위 (상자 내 제1·2·3사분위수 표시)
제1사분위 : 작은 쪽 부터 세었을 때 1/4 위치에 있는 값
제2사분위 : 중앙값(median)
제3사분위 : 큰 쪽부터 세었을 때 1/4 위치에 있는 값
- 수염 : 상자 길이(IQR)의 1.5배 범위 안에서, 최대값·최소값 (수염에 포함되지 않은 값은 이상값으로 정의)

* IQR(사분위수 범위, InterQauntile Range)
② 막대그래프(평균값) + 오차 막대(S.D.)
- 막대그래프의 높이 : 평균값, 오차 막대 : 표준편차(S.D.)
- 분포 형태까지는 자세하게 알 수 x
*추론통계에서 S.D.가 아닌 표준오차(standard error, S.E.)를 오차 막대로 그릴 때가 많음; 범례에 오차 막대가 무엇을 나타내는지 반드시 표시
③ 바이올린 플롯(violin plot)
- 히스토그램을 부드럽게 표현; 핵밀도 추정을 통해 어디쯤 데이터가 존재하기 쉬운지를 추정하여 나타냄
*핵밀도 추정(kernel density estimation) : 관측된 데이터를 바탕으로 관심 대상인 확률 변수가 특정 분포를 따른다는 가정 하에 확률 밀도를 추정하는 방법
④ 스웜 플롯(swarm plot)
- 값이 겹치지 않도록 점을 찍음; 각 데이터가 어디에 있는지 자세하게 나타냄
- 평균값·중앙값 등의 통계량 표시x, BUT 분포 형태·자세한 데이터 위치 정보 시각화o
⑤ 상자 수염 그림 + 스웜 플롯
- 평균값·중앙값 등의 통계량 표시o, 분포 형태·자세한 데이터 위치 정보 시각화o
7) 이상값
평균값에서 표준편차의 2 or 3배 이상 벗어난 숫자
ex : 평균 50, 표준편차 15인 시험 점수 데이터 분포
- 20점 이하, 80점 이상 이상값 (표준편차 2배 기준)
- 5점 이하, 95점 이상 이상값 (표준편차 3배 기준)
출처 : ⎡통계101 x 데이터 분석 (아베 마사토)⎦, [지니Go수학] 상자그림, 상자수염그림, bo.. : 네이버블로그 (naver.com)
'통계학 > 03. 통계분석의 기초' 카테고리의 다른 글
| 03-4 이론적인 확률분포 (0) | 2024.06.11 |
|---|---|
| 03-3 확률 (1) | 2024.06.11 |
| 03-1 데이터 유형・분포 (0) | 2024.06.09 |

