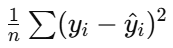[천재교육] 프로젝트 기반 빅데이터 서비스 개발자 양성 과정 9기
학습일 : 2024.09.04
📕 학습 목록
- 퍼셉트론
- 비용 함수
- 활성화 함수
- 경사하강법
📗 기억할 내용
1. 퍼셉트론 (Perceptron)
1) 논리 게이트
① 정의
- 주어진 입력에 대해 특정 논리 연산(AND, OR, NOT 등)을 수행하는 디지털 회로
- ex : AND 게이트_두 입력이 모두 참(True)일 때만 참을 출력 / OR 게이트_하나라도 참이면 참을 출력
- 퍼셉트론이 수행할 수 있는 가장 기본적인 연산의 예
- 논리 게이트 구현
- AND(곱셈 연산) : 두 입력값 A와 B가 모두 1일 때만 출력값 F=1
- OR(덧셈 연산) : A 또는 B 중 하나라도 1이면 출력값 F=1
- NAND(부정 AND) : A와 B가 모두 1인 경우를 제외하고 출력값 F=1(AND 연산의 결과를 뒤집은 것)
- XOR(배타적 OR) : A와 B가 서로 다를 때만 출력값 F=1
- NOT(부정 연산) : 입력값을 뒤집음
- XNOR : XOR의 반대, A와 B가 같을 때 출력값 F=1

2) 단층 퍼셉트론
① 정의
- 퍼셉트론 : 입력에 가중치를 적용해 활성화 함수를 통과시켜 이진 출력을 내는 인공 신경망의 기본 단위
- 퍼셉트론 학습 원리 : 가중치&활성화 함수를 사용하여 학습을 수행 → 결과를 바탕으로 모델을 개선
- 단층 퍼셉트론(Single-Layer Perceptron) : 입력층과 출력층으로만 구성된 신경망으로, 선형 분류 문제를 해결할 수 있는 모델


② 한계 : XOR와 같은 비선형 분류 문제는 해결 불가

3) 다층 퍼셉트론
① 정의
- 다층 퍼셉트론(Multi-Layer Perceptron) : 입력층, 은닉층, 출력층으로 이루어진 신경망으로, 비선형 문제까지 해결 가능한 복잡한 모델

| 논리 게이트 | 단층 퍼셉트론 | 다층 퍼셉트론 | |
| 정의 | AND, OR, NOT 등 논리 연산을 수행하는 디지털 회로 | 단일 계층으로 이루어진 인공 신경망의 기본 단위 | 여러 개의 퍼셉트론이 계층적으로 연결된 인공 신경망 (MLP) |
| 구조 | 고정된 논리 회로로 이루어짐 | 입력층과 출력층으로 구성, 은닉층은 없음 | 입력층, 은닉층(하나 이상), 출력층으로 구성됨 |
| 대표 이미지 |
 |
 |
 |
| 입력과 출력 |
이진 값(0, 1) | 이진 값 또는 실수 값 | 이진 값 또는 실수 값 |
| 계산 방식 | 논리 연산 (AND, OR, NOT 등) | 가중치와 바이어스를 이용해 선형 분류 | 여러 계층을 통해 비선형 분류 가능 |
| 구현 가능 연산 | 선형적으로 구분 가능한 논리 연산만 수행 (AND, OR, NOT 등) | 선형적으로 구분 가능한 문제 해결 가능 (AND, OR, NOT) | 비선형적으로 구분 가능한 문제 해결 가능 (XOR 포함) |
| 학습 능력 | 고정된 연산, 학습 불가 | 학습 가능 (가중치와 바이어스 업데이트) | 더 복잡한 학습 가능 (역전파 알고리즘을 통해 다층 학습) |
| 복잡성 | 매우 단순 | 단순한 모델 | 복잡한 모델 |
| 대표적 사용 예시 |
간단한 디지털 회로 (CPU, 메모리 등) | 단순한 분류 문제, 논리 게이트 구현 | 이미지 인식, 음성 인식, 자연어 처리 등 복잡한 문제 해결 |
| 한계 | 비선형 문제(XOR 등)는 해결할 수 없음 | XOR와 같은 비선형 문제는 해결할 수 없음 | - |
2. 비용 함수 (Loss Function)
1) 비용 vs 오차
| 비용(= 손실, Loss) | 오차(Error) | |
| 정의 | 모델의 예측값과 실제값 사이의 평균적인 오차를 측정하는 값 | 모델의 예측값과 실제값 사이의 차이 |
| 수식적 의미 | 비용 함수에 의해 계산된 평균적인 오차 | 단일 예측에 대한 실제값과 예측값 간의 차이 |
| 사용 목적 | 모델 학습 중 가중치를 최적화하기 위해 사용하는 평가 기준 | 개별 데이터 포인트에서의 예측 성능을 평가하기 위해 사용 |
| 계산 방식 | 비용 함수(MSE, MAE 등)를 사용해 모든 데이터 포인트에서 평균 계산 | 단일 예측값과 실제값 간의 차이를 사용 |
| 범위 | 주로 여러 데이터 포인트에서 평균적인 성능 평가 | 단일 예측 또는 하나의 데이터 포인트에서의 차이를 평가 |
| 예시 | MAE, MSE, RMSE, Cross-Entropy 등 다양한 비용 함수 사용 | 즉, 오차 값 자체 |
| 종류 | MAE, MSE, RMSE, Cross-Entropy 등 | 절대 오차, 제곱 오차 등 여러 형태로 표현 가능 |
| 모델 학습 에서의 역할 |
비용은 여러 데이터 포인트에서의 오차를 종합하여 학습 중 최적화 대상이 됨 | 오차는 개별 데이터 포인트에 대해 평가하며 비 계산에 사용됨 |
| 예시 상황 | 모델 학습 중 비용 값을 줄여가며 성능을 최적화함 | 특정 데이터 포인트에서 예측이 얼마나 잘 되었는지를 확인할 때 사용 |
2) 비용 함수
① 정의
- 모델의 예측값과 실제값의 차이를 계산하는 함수; 모델의 성능을 평가하는 데 사용됨
② 종류
| 비용 함수 |
||||
| MAE | MSE | RMSE | Cross Entropy | |
| 정의 | 예측값과 실제값 간의 절대 오차의 평균 | 예측값과 실제값 간의 제곱 오차의 평균 | 평균 제곱 오차(MSE)의 제곱근 | 예측 확률과 실제 레이블 간의 차이를 측정 |
| 설명 | 절대 오차이므로 오차의 크기를 동일하게 처리 | 오차를 제곱하여 큰 오차에 더 큰 패널티 부여 | 오차를 제곱한 후 다시 제곱근을 구하여 원래 단위로 복원 | 실제 확률 분포 p(xi) 와 예측 확률 분포 q(xi) 의 차이를 측정 |
| 특징 | 모든 오차를 동일하게 취급하며 큰 오차에 덜 민감함 | 큰 오차에 매우 민감함 | 큰 오차에 민감하면서도, 실제 오차 크기와 같은 단위를 유지 | 확률이 크게 벗어난 예측에 큰 페널티 부여; 확률적 예측의 성능을 평가 |
| 오차 처리 | 큰 오차와 작은 오차를 동일하게 처리 | 큰 오차에 더 큰 패널티(가중치)를 부여 | 큰 오차에 민감하지만 실제 데이터 단위로 처리 | 확률이 크게 벗어난 경우 큰 페널티를 줌 |
| 사용 예시 | 회귀 분석에서 많이 사용되며, 쉽게 해석 가능 | 회귀 분석에서 주로 사용, 큰 오차를 더 크게 처리하고 싶을 때 유용 | MSE의 단위 문제를 해결하며 해석 가능성 높임 | 분류 문제에서 주로 사용, 이진/다중 클래스 분류에 적합 |
| 수식 |  |
|||
3. 활성화 함수 (= 비선형 변환 함수, Activation Function)
① 정의
- 인공 신경망에서 입력 신호를 처리하고, 그 결과를 다음 층으로 전달할지 여부를 결정하는 함수
- 입력 신호를 비선형적으로 변환하여 신경망이 복잡한 패턴을 학습할 수 있도록 도와줌
- 학습 과정에서 신경망의 성능에 큰 영향을 미침
② 종류
| 활성화 함수 | |||||||
| ReLU | Leaky ReLU | Sigmoid | Tanh | Softmax | ELU | GELU | |
| 정의 | 입력값이 0보다 크면 그대로 출력하고, 작으면 0을 출력 | ReLU의 변형, 음수 값에 대해 일정한 기울기를 가짐 | 모든 실수 입력값을 0과 1 사이로 압축 | Sigmoid와 유사하지만, 출력값의 범위가 -1에서 1 사이 | 다중 클래스 분류에서 각 클래스에 속할 확률을 출력 | ReLU와 비슷하지만 0 이하 값에 대해 음의 값을 허용 | 입력값을 가우시안 분포를 기반으로 비선형적으로 변환 |
| 수식 |  |
 |
 |
 |
 |
 |
 |
| 특징 | - 계산이 매우 간단하고 효율적 - 비선형성을 제공하지만, 죽은 ReLU 문제 발생 가능 |
ReLU의 장점을 유지하면서도, 음수 입력에서도 작은 기울기를 가져 가중치가 업데이트 가능 | 출력값이 확률로 해석 가능하지만, 기울기 소실 문제 발생 가능 | - 음의 값을 허용하며, 출력값이 0에 가까울 때 기울기가 큼 - 하지만 기울기 소실 문제 발생 가능 | 각 클래스에 대한 확률 분포를 출력하여 모든 확률값의 합이 1이 되도록 만듦 | - 음의 값에서도 기울기를 유지해 '죽은 ReLU' 문제 방지 - 학습이 더 안정적이고 빠름 |
ReLU보다 부드러운 함수로 자연어 처리(NLP) 분야에서 많이 사용 |
| 주요 사용처 | 대부분의 은닉층에서 널리 사용 | ReLU의 대안으로 사용, 죽은 ReLU 문제 방지 | 이진 분류 문제에서 주로 사용 (출력층) | 은닉층에서 가끔 사용, 출력값이 -1에서 1 사이일 때 유리 | 다중 클래스 분류 문제의 출력층 | ReLU의 개선된 버전으로, 성능이 더 나은 경우 사용 | 트랜스포머 모델과 같은 최신 아키텍처에서 주로 사용 |
4. 경사하강법 (Gradient Descent)
1) 정의
- 비용 함수의 기울기를 계산하여, 기울기가 가리키는 방향으로 점진적으로 이동함으로써 손실을 최소화하는 방식
- 기계 학습 및 최적화 알고리즘에서 매우 중요한 방법으로, 주어진 함수의 최소값을 찾기 위해 사용됨
2) 작동 과정
① 손실 함수(Loss Function) : 주어진 문제에서 목표는 모델이 예측한 값과 실제 값의 차이를 최소화하는 것. 이 차이는 손실 함수로 계산됨
② 기울기(Gradient) 계산 : 경사하강법에서는 손실 함수의 기울기를 계산하여, 이 기울기가 가리키는 방향으로 손실을 줄이기 위한 움직임을 결정
- 기울기가 양수이면, 가중치(파라미터)를 감소시킴
- 기울기가 음수이면, 가중치를 증가시켜 손실을 줄임
③ 학습률(Learning Rate) : 경사하강법에서 매번 기울기 방향으로 이동할 때, 얼마나 많이 이동할지를 결정하는 파라미터. 학습률이 너무 크면 최적해를 넘어서 버릴 수 있고, 너무 작으면 학습이 매우 느려질 수 있음
④ 업데이트 : 매 반복마다 가중치를 다음과 같이 업데이트함

⑤ 반복 : 손실 함수가 충분히 줄어들 때까지, 즉 기울기가 0에 가까워질 때까지 이 과정을 반복
3) 종류
| 경사하강법 | |||
| 배치 경사하강법 (Batch Gradient Descent) |
확률적 경사하강법 (Stochastic Gradient Descent, SGD) |
미니배치 경사하강법 (Mini-Batch Gradient Descent) |
|
| 정의 | 전체 데이터셋을 사용하여 기울기를 계산하는 방법 | 데이터셋에서 무작위로 하나의 데이터 포인트만을 사용해 기울기를 계산 | 데이터셋을 작은 배치로 나누어 각 배치에 대해 기울기를 계산하는 방법 |
| 장점 | 기울기 계산이 정확함 | 계산 속도가 매우 빠름 | 배치와 확률적 경사하강법의 장점을 결합해 안정성과 속도를 동시에 제공 |
| 단점 | 대규모 데이터셋에서는 계산 비용이 많이 듬 | 기울기의 변동이 커서 최적화 경로가 불안정할 수 있음 | 배치 크기 설정이 필요하며, 적절한 배치 크기를 찾지 않으면 성능 저하 가능 |
| 학습 속도 | 느림 | 빠름 | 배치 크기에 따라 다름 |
| 메모리 요구량 | 큼 | 작음 | 중간 |
| 최적화 경로의 안정성 | 매우 안정적 | 불안정할 수 있음 | 안정적이나 일부 변동 존재 |
| 사용 예 | 데이터셋이 작거나 계산 비용을 감수할 수 있는 경우 | 대규모 데이터셋에서 빠른 학습이 필요할 때 | 딥러닝 모델 학습에서 일반적으로 사용됨 |
4) 문제점 및 해결방법
- 학습률 설정의 어려움 : 학습률이 너무 크면 발산하고, 너무 작으면 수렴 속도가 느려짐
- Sol) 모멘텀(Momentum) or 적응형 학습률(Adam) 같은 최적화 기법을 사용
- 지역 최솟값(Local Minima) : 손실 함수의 전역 최솟값이 아닌 지역 최솟값에 빠질 수 있음
- Sol) 모멘텀 기법을 사용하면 경사가 급격하게 바뀌는 부분에서 부드럽게 최솟값을 찾아가도록 할 수 있음
- 기울기 소실 문제 : 신경망이 깊어질수록 기울기가 점점 작아져, 가중치가 거의 업데이트되지 않는 현상
- Sol) ReLU 같은 활성화 함수를 사용 or 배치 정규화(Batch Normalization)를 사용해 기울기 소실 문제를 완화
5) 경사하강법 최적화 기법
- 모멘텀 (Momentum) : 기존 경사하강법에 관성을 추가하여, 기울기가 0에 가까워질수록 점진적으로 움직임을 줄이는 방식. 학습률을 개선하고, 지역 최솟값에 빠지지 않도록 도와줌
- Adam (Adaptive Moment Estimation) : 학습률을 자동으로 조정해주는 알고리즘으로, 각 파라미터에 대해 적응적으로 학습률을 조정하여 빠른 수렴을 유도
- RMSprop : 각 변수에 대해 학습률을 다르게 조정해, 경사가 급한 방향과 완만한 방향에서 학습률을 다르게 적용하는 방법
📙 내일 일정
- 딥러닝 기본 개념

'TIL _Today I Learned > 2024.09' 카테고리의 다른 글
| [DAY 41] Deep Learning 실습 (0) | 2024.09.09 |
|---|---|
| [DAY 40] Deep Learning 실습 (0) | 2024.09.06 |
| [DAY 39] Deep Learning 실습 (0) | 2024.09.05 |
| [DAY 37] 딥러닝 프레임워크 (5) | 2024.09.03 |
| [DAY 36] Machine Learning 실습 (0) | 2024.09.02 |