[천재교육] 프로젝트 기반 빅데이터 서비스 개발자 양성 과정 9기
학습일 : 2024.08.20
📕 학습 목록
- 머신러닝 분류/회귀 모델
📗 기억할 내용
1. 머신러닝 분류 모델
1) 분류 (Classification)
- 머신러닝 알고리즘을 통해 데이터's feature(독립변수)/label(종속변수) 값을 학습 → 모델(객체) 생성 → 모델에 새로운 데이터 값이 주어졌을 때 미지의 label 값을 예측하는 것
2) 분류 모델 (Classification Model) : 이진분류기, 다항분류기, 결정 트리 분류기
① 이진분류기(Binary Classifier) 분류 모델 : 입력된 데이터를 두 그룹(참 or 거짓)으로 분류
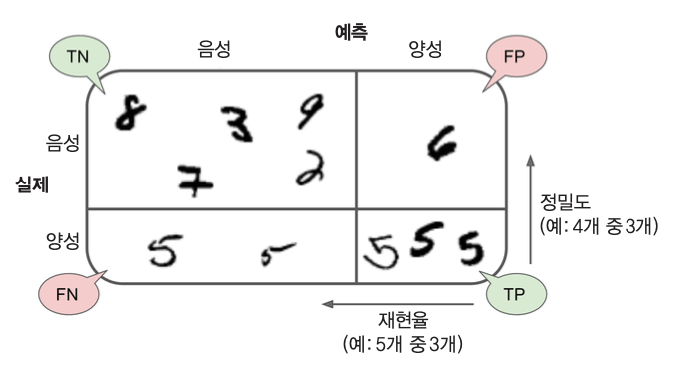
- 분류 평가 지표 : 오차행렬, F1 점수, Precision & Recall Trade-off, ROC "이진분류가 잘 되었는지 확인"
2-1) 오차 행렬(Confusion Matrix) 평가 지표 : 레이블 별 예측 결과를 정리한 행렬
- 참 : 숫자 5를 가리키는 이미지 / 거짓 : 그 외의 수를 가리키는 이미지
- 머신러닝 모델 평가기준; 목적에 따라 Precision 과 Recall의 중요도가 다름
(i) Recall > Precision
- 암 진단 기준 : 실제 암인 사람에게 암이라고 진단한 비율 “참중에 참을 몇개 찾았나”
(ii) Precision > Recall
- 아동용 동영상 선택 기준 : 안전한 동영상 중 실제로 안전한 동영상의 비율 “거짓+참 중에 참을 몇개 찾았나”
2-2) F1 점수 평가 지표 : 정밀도(Precision) & 재현율(Recall)의 조화 평균
- F1 점수는 Precision과 Recall 간의 균형을 평가하여, 두 지표의 trade-off(상호 반비례 관계)를 직접 반영
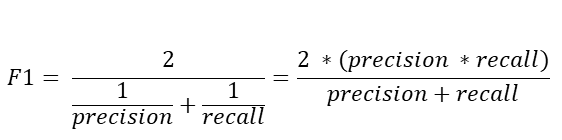
2-3) Precision & Recall Trade-off 평가 지표 : 정밀도 - 재현율 사이의 균형맞추기
- 결정임계값 (Decision Threshold) : 분류 모델에서 예측 확률을 실제 클래스 레이블로 변환할 때 사용하는 기준값
- 결정임계값을 조정하여 정밀도와 재현율의 trade-off를 조절; 최적의 임계값 선택
- 결정임계값을 높이 설정할수록, Precision↑ • Recall↓

2-4) ROC(Receiver Operating Characteristic) 곡선 평가 지표 : FP Rate에 대한 TP Rate의 관계를 나타냄
* FP Rate : 거짓 양성 비율
FPR = FP / (FP + TN)
* TP Rate : 참 양성 비율(=Recall)
TPR = Recall = TP / (TP + FN)
[좋은 성능의 분류기 기준]
- 거짓 양성비율(X축) ↓ Recall(y축) ↑ 하게 유지
- ROC 커브가 y축에 최대한 근접
- AUC가 1에 가까움

② 다항분류기 (Multiclass Classifier) 분류 모델 : 입력된 데이터를 세개 이상의 클래스로 분류
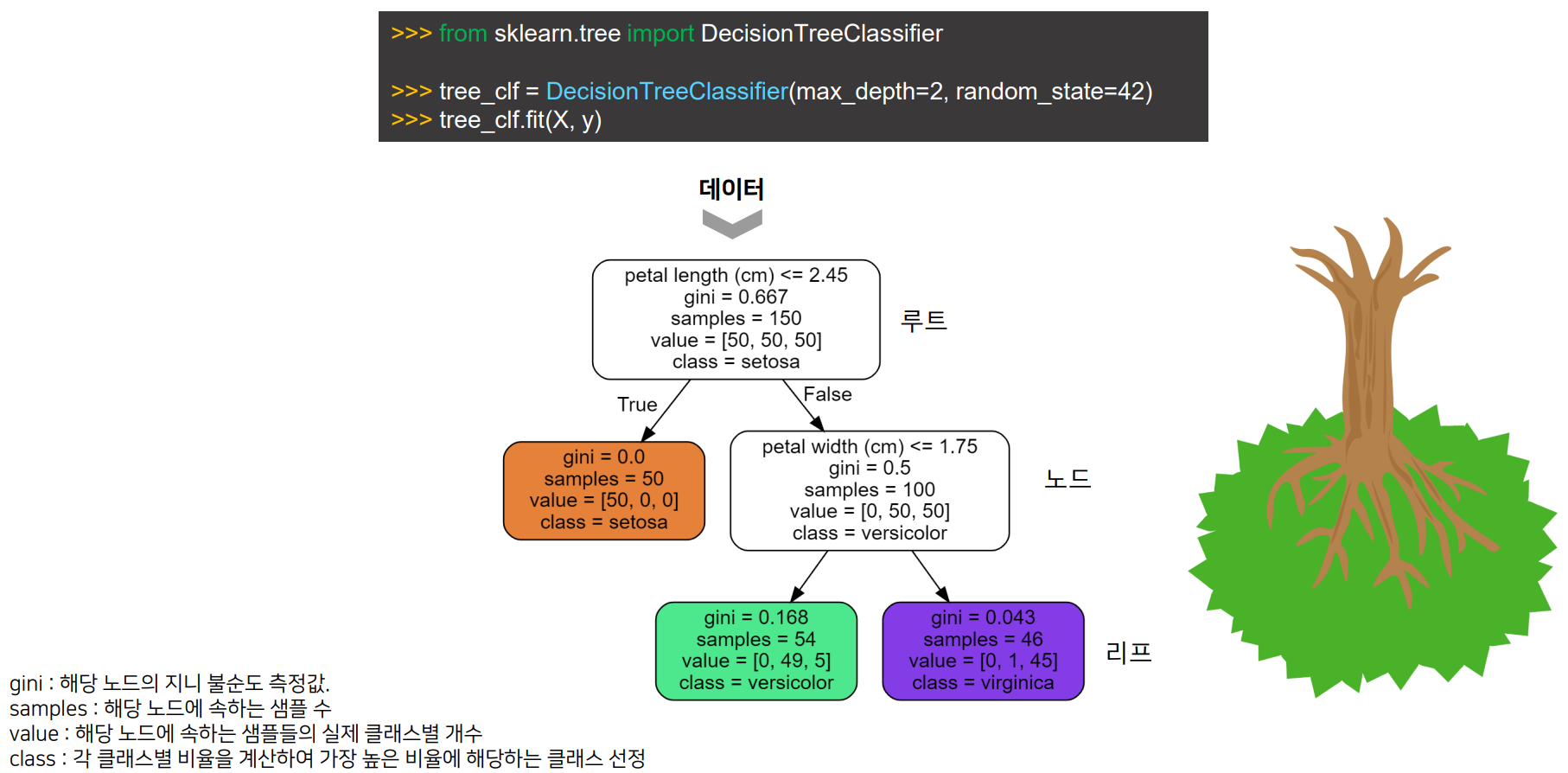
③ 결정 트리 분류기 (DecisionTreeClassifier) 분류 모델
- sklearn의 class
- 결정 트리(Decision Tree) 알고리즘을 사용하는 분류기
- 주어진 입력 데이터에 대해 클래스 레이블을 예측하는 데 사용됨

- 결정 트리(Decision Tree) 알고리즘
- 데이터의 특성에 따라 의사결정을 나무 형태로 모델링하는 기계 학습 알고리즘
- 데이터에 있는 규칙을 학습을 통해 자동으로 찾아냄 → 트리 기반의 분류 규칙(if - else 기반)을 생성
- 매우 쉽고 유연하게 적용될 수 있는 알고리즘
- 결정트리 장점/단점
[장점]
- 이해하기 쉬움. 직관적
- 모델을 시각화할 수 있음; 화이트 박스 모델을 적용할 수 있음
- 데이터 전처리를 거의 요구하지 않음
- 모델의 복잡도가 데이터의 복잡도에 비례; 학습에 소요되는 자원을 예측하기 쉬움
- 숫자형 및 범주형 데이터 모두 사용 가능
[단점]
- 과적합으로 성능이 떨어질 수 있음(규제 필요)
- 입력 데이터의 차이가 조금만 나더라도 트리가 크게 달라질 수 있음
- 외삽(입력 값의 범위 바깥에서 추정하는 작업)에 적합한 모델은 아님
- 최적의 의사결정나무 모델 학습은 NP-완전 문제; 즉, 최적의 알고리즘이 발견되지 않은 상황
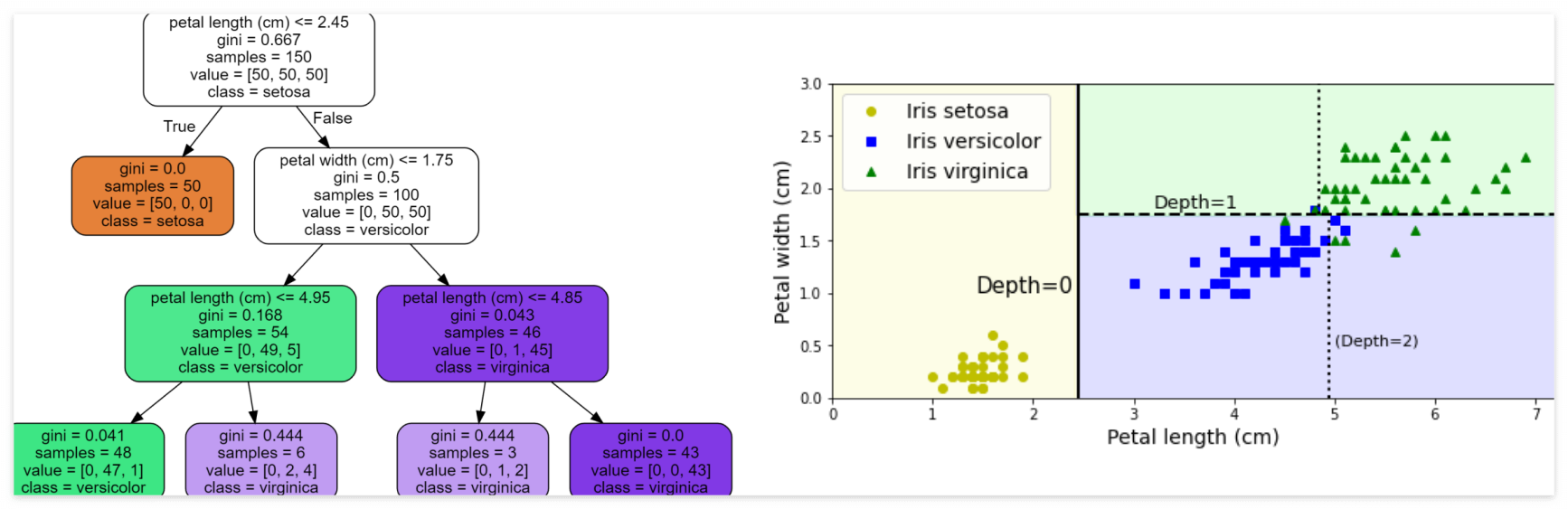
- gini 하이퍼파라미터
- 결정트리의 분리가 잘 된 것을 평가하기 위한 지표; 불순도를 측정함
- 0에 가까울 수록, 해당 클래스에 섞인 다른 클래스의 양이 적음을 의미
* 조건부 확률 p(j | t) : 현재 노드 t에서 클래스(라벨) j에 속하는 샘플의 비율
* c : 클래스의 총 수
ex : 노드 t에 샘플 100개가 존재. 이중 70개가 클래스 A에 속함 & 30개가 B에 속함.
-> 클래스 A에 대한 비율 p(A | t) = 70/100 = 0.7
-> 클래스 B에 대한 비율 p(B | t) = 30/100 = 0.3
=> 불순도 G(t) = 1 - (0.7^2 + 0.3^2) = 1 - (0.49 + 0.09) = 1 - 0.58 = 0.42


- 규제 하이퍼파라미터
- max_depth : 결정트리의 높이 제한
- min_samples_split : 노드 분할에 필요한 최소 샘플 개수
- min_samples_leaf : 리프에 포함된 최소 샘플 개수
- min_weight_fraction_leaf : 샘플 가중치 합의 최솟값
- max_leaf_nodes : 최대 리프 개수
- max_features : 분할에 사용되는 특성 개수

3) 알고리즘 : 지도/비지도/강화/앙상블 학습 알고리즘
- 데이터를 이용해 모델을 학습하고 예측이나 분류와 같은 작업을 수행하는 절차나 방법
| 학습 방법론 | 작업 유형 | 알고리즘 | 설명 |
| 지도 학습 * 분류 : 이산적인 카테고리 값 예측 * 회귀 : 연속적인 값 예측 |
이진 분류 |
로지스틱 회귀 | 선형 모델로 이진 분류 수행 |
| 서포트 벡터 머신(SVM) | 최적의 초평면을 통해 이진 분류 수행 | ||
| 결정 트리 | 트리 구조를 통해 이진 분류 수행 | ||
| K-최근접 이웃(KNN) | 이웃 K개를 기반으로 이진 분류 | ||
| 나이브 베이즈 | 조건부 확률에 기반한 이진 분류 | ||
| 신경망 (MLP) | 다층 퍼셉트론 구조로 복잡한 이진 분류 수행 | ||
| 다중 클래스 분류 |
소프트맥스 회귀 | 다중 클래스 로지스틱 회귀, 다중 클래스 분류에 사용 | |
| 다중 클래스 SVM | 여러 SVM을 조합하여 다중 클래스 분류 수행 | ||
| 결정 트리 | 트리 구조를 통해 다중 클래스 분류 수행 | ||
| 랜덤 포레스트 | 여러 결정 트리를 앙상블하여 다중 클래스 분류 성능 향상 | ||
| 나이브 베이즈 | 조건부 확률에 기반한 다중 클래스 분류 | ||
| 신경망 (MLP) | 다층 퍼셉트론 구조로 복잡한 다중 클래스 분류 수행 | ||
| 선형 판별 분석(LDA) | 클래스 간 분산을 최대화하여 다중 클래스 분류 | ||
| 회귀 |
선형 회귀 | 종속 변수와 독립 변수 간의 선형 관계를 모델링 | |
| 릿지 회귀, 라쏘 회귀 | 규제를 추가한 선형 회귀로 과적합 방지 | ||
| 다항 회귀 | 비선형 관계를 다항식으로 모델링하는 회귀 방법 | ||
| 신경망 (MLP) | 복잡한 비선형 관계를 모델링하는 회귀에 사용 | ||
| 비지도 학습 | 클러스터링 | K-평균 (K-Means) | 데이터를 K개의 클러스터로 그룹화 |
| 계층적 클러스터링 | 데이터의 계층 구조를 기반으로 클러스터링 수행 | ||
| DBSCAN | 밀도 기반 클러스터링, 노이즈를 처리 가능 | ||
| 가우시안 혼합 모델(GMM) | 데이터가 여러 가우시안 분포에서 생성된 것으로 가정 | ||
| 차원 축소 | 차원 축소 | 주성분 분석(PCA) | 데이터의 분산을 최대화하는 방향으로 차원 축소 |
| 선형 판별 분석(LDA) | 클래스 간 분리를 극대화하는 방향으로 차원 축소 | ||
| 강화 학습 | 제어 및 최적화 | Q-러닝 | 상태-행동 페어에 대한 가치를 학습하는 기법 |
| 딥 Q-네트워크(DQN) | 신경망을 사용한 Q-러닝 기법 | ||
| 앙상블 학습 | 분류 (이진/다중 클래스) |
랜덤 포레스트 | 여러 결정 트리를 앙상블하여 분류 성능 향상 |
| 부스팅 (XGBoost, LightGBM, CatBoost) | 약한 학습기들을 결합하여 강력한 예측 모델 생성 | ||
| 배깅 (Bagging) | 여러 모델을 독립적으로 학습시켜 결합하는 방법 | ||
| 보팅 (Voting) | 여러 모델의 예측 결과를 투표하여 최종 예측 결정 | ||
| 스테킹 (Stacking) | 여러 모델의 예측을 메타 모델에 입력하여 최종 예측 수행 |
① KNN (K-Nearest Neighbor) 알고리즘
- 주변 데이터(neighbor)를 살펴본 뒤 더 많은 데이터가 포함되어 있는 클래스로 분류
- 주변의 데이터를 K개 살펴봄
- 학습이 필요없음 (lazy model)

- KNN에서 사용하는 거리 측정법 : 유클리드 거리(Euclidean Distance)
- 일반적으로 가장 많이 사용하는 거리 척도
- 서로 다른 관측치 x, y 값 간 차이 제곱합의 제곱근 (= 두 관측치 사이의 직선거리)



② 앙상블 학습 방법론 : 여러개의 분류기를 생성 → 예측들을 결합 → 보다 정확한 예측 도출
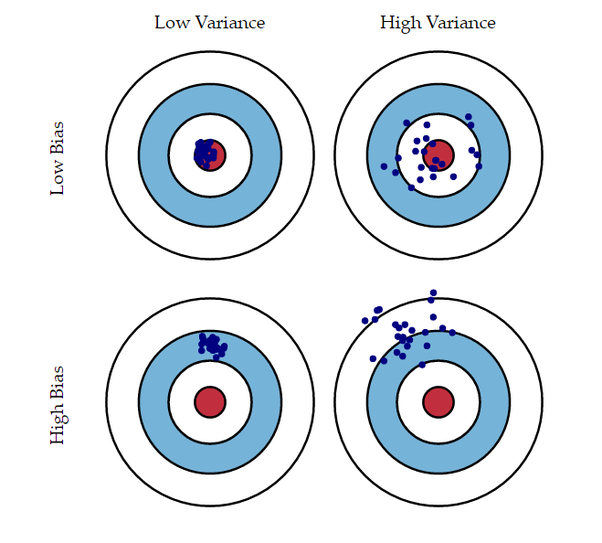
* 앙상블 핵심 : 편향&분산을 줄인 모델 구현
- 강력한 하나의 모델을 사용하는 대신, 약한 모델 여러개를 조합 → 더 정확한 예측
- 앙상블 학습 ⊃ 보팅, 배깅, 부스팅
- 편향(Bias) : 예측값과 정답이 떨어져 있는 정도
- 정답에 대한 가정으로 부터 유발
- 편향↑ → 과소적합
- 분산(Variance) : 입력 샘플의 작은 변동에 반응하는 정도
- 정답에 대한 너무 복잡한 모델을 설정하는 경우 분산↑
- 분산↑ → 과대적합
- 보팅(Voting) 알고리즘 : 여러 분류기가 투표를 통해 최종 예측 결과를 결정. 서로 다른 알고리즘을 여러개 결합하여 사용
- 하드 보팅 : 다수의 분류기가 예측한 결과값을 최종 결과로 선정
- 소프트 보팅 : 모든 분류기가 예측한 레이블 값의 결정 확률 평균을 구한 뒤 가장 확률이 높은 레이블 값을 최종 결과로 선택

- 배깅(Bagging) 알고리즘 : 데이터 샘플링을 통해 모델을 학습시키고, 결과를 집계
- Bagging: Bootstrap Aggregation의 줄임말
* Bootstrap: 원본 데이터셋에서 중복을 허용하여 여러 번 리샘플링하는 방법
- Bagging은 모두 같은 유형의 알고리즘을 기반으로 한 여러 개의 분류기를 사용
- 각 분류기의 예측값 중 최빈값(다수결 투표)을 최종 예측값으로 선택
- 데이터를 여러 번 샘플링하여 다양한 표본을 생성함으로써, 모델의 분산을 줄이는 효과를 얻음. 다양한 표본은 모델이 특정 데이터에 과적합되지 않도록 함
- Bagging 대표 예 : 랜덤 포레스트 알고리즘


- 랜덤 포레스트 (Random Forest) 알고리즘 : 배깅 기법을 결정트리의 앙상블에 특화시킨 모델

- Feature Importance : 기계 학습 모델에서 각 특성(Feature)이 모델의 예측에 기여하는 정도를 나타내는 지표

- 부스팅(Boosting) 알고리즘
- 여러 개의 분류기가 순차적으로 학습
- 예측이 틀린 데이터에 대해 이전 분류기가 올바르게 예측할 수 있도록 다음 분류기에게 가중치를 부여
- 계속 가중치를 부여해가며 학습을 진행 "부스팅"
- 배깅 방식과는 달리 훈련을 동시에 진행할 수 x (∵ 순차적)
- 부스팅 ⊃ 에이다 부스트, 그래디언트 부스팅
- 에이다부스트 (AdaBoost) 알고리즘
- 하나의 모델을 훈련시킨 후 잘못 예측된 샘플을 더 강조 ↑ → 해당모델을 다시 훈련시킴

- 그래디언트 부스팅 (Gradient Boosting) 알고리즘
- 이전 모델의 예측에 오차가 있다면 → 그 오차를 보정하는 새로운 예측기를 새롭게 훈련시킴
- 이전 예측기에 의해 생성된 잔차(residual error)에 대해 새로운 예측기를 학습시킴 (≠ 에이다부스트 : 샘플의 가중치를 조정)

- 스태킹(Stacking) 알고리즘
- 배깅방식의 응용
- 다수결을 이용하는 대신, 여러 예측값을 학습데이터로 활용하는 예측기를 학습시

2. 머신러닝 회귀 모델
1) 회귀
① 회귀란?
- '여러 개의 독립변수 - 한 개의 종속변수' 간의 상관관계를 모델링하는 기법을 통칭
- 회귀 계수 W : 가중치
- 머신러닝 회귀 예측's 핵심 : 학습을 통해 최적의 회귀계수를 찾아내는 것

② 회귀 유형
| 독립변수 개수 | 회귀 계수의 결합 |
| 1개 : 단일 회귀 | 선형 : 선형 회귀 |
| 2개 이상 : 다중 회귀 | 비선형 : 비선형 회귀 |
2) 선형 회귀
- 최적의 회귀모델 : 전체 데이터의 잔차(오류값) 합이 최소가 되는 모델을 만듦


① 회귀 모델 성능 평가 지표 : MSE
- MSE (Mean Square Error) : 작을수록 좋음


- MSE가 최소가 되도록 하는 파라미터를 찾는 것이 최종 목표 by 정규방정식, SVD, 경사하강법
- MSE 단점 : 제곱이 있어 숫자가 너무 커질 수 있음 -> 루트 씌워서 평가 "RMSE(Root Mean Square Error)"
①-1 정규방정식
- 편미분 했을 때, 기울기가 0이될 때 "최적의 방법"

①-2 SVD (특이값 분해, Singular Value Decomposition)

→ Sklearn : 최적의 θ 를 계산하는 LinearRegression 클래스 제공 → 객체(회귀 모델) 생성
import numpy as np
from sklearn.linear_model import LinearRegression
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
# y = 1 * x_0 + 2 * x_1 + 3
y = np.dot(X, np.array([1, 2])) + 3
reg = LinearRegression().fit(X, y
①-3 경사하강법 ⊃ 배치 경사하강법, 확률적 경사하강법(SGD)
- training set을 이용하는 학습 과정 중, 가중치 파라미터를 조금씩 반복적으로 조정; Cost의 크기를 줄이는 방향으로 조정
* 비용함수(Cost function)
- 오차를 대변하는 숫자(≒ MSE)
- 모델의 성능을 평가하기 위해 사용되는 함수(작을수록 좋음)
- 모델의 예측값과 실제값 간의 오차를 측정하여, 모델이 얼마나 잘 작동하고 있는지를 수치적으로 표현


- 진행과정
- 학습 스텝 : 적당히 간격을 두기
(i) 스텝 크기 ↑ : 편미분을 더 넓은 범위에서 진행 → 속도 빠르나, 최적의 값을 지나칠 수 있음
(ii) 스텝 크기 ↓ : 학습을 너무 많이 진행하게되나, 최적의 값을 지나칠 가능성↓

- 주의사항
| 그래프 | 설명 |
| 왼쪽 위 | 학습 스텝이 너무 작음: 학습 스텝 크기가 너무 작아서 모델이 최솟값에 천천히 수렴. 학습이 오래 걸리며, 비효율적 |
| 왼쪽 아래 | 학습 스텝이 너무 큼: 학습 스텝 크기가 너무 커서 최솟값으로 수렴하지 않고, 오히려 발산함. 최적의 값을 찾지 못하고 학습이 실패할 수 있음 |
| 오른쪽 아래 | 학습이 특정 지역에 갇힘 : 지역 최솟값에 빠지거나, 평지(기울기가 0인 지점)에서 정지해버림. 전역 최솟값에 도달하지 못할 수 있음 |

- 경사하강법 종류 : 모델에 지정하는 배치 크기에 따라 3가지(배치 경사하강법, 확률적 경사하강법, 미니 배치 경사하강법)로 나뉨
| 용어 | 정의 | 관계 |
| 배치 | 한 번의 업데이트에 사용되는 데이터의 개수 | 배치 크기가 클수록 한 에포크 당 스텝 수는 줄어듦 |
| 스텝 | 한 번의 파라미터 업데이트 과정 | 한 에포크 = 데이터셋 크기 / 배치 크기 × 스텝 수 |
| 에포크 | 전체 데이터셋이 한 번 모델을 통해 학습되는 과정 | 여러 에포크 동안 학습하며, 각 에포크는 여러 스텝으로 구성됨 |
- ex : 학습 데이터 1000개 & 배치크기 10 → 총 100번의 스텝 실행됨

- 전체 배치 경사하강법 : 전체 데이터셋을 사용하여 한 번에 경사를 계산하고 파라미터를 업데이트함. 수렴이 안정적이지만, 데이터셋이 클 경우 계산이 느

- 확률적 경사하강법(SGD) : 하나의 데이터 포인트만을 사용하여 경사를 계산하고 파라미터를 업데이트함. 빠르게 수렴하지만, 수렴 과정에 노이즈가 많음

- 미니 배치 경사하강법 : 위 두 방법의 절충안으로, 작은 배치 단위로 경사를 계산하고 파라미터를 업데이트하여, 계산 효율성과 수렴 안정성 간의 균형을 맞춤

3) Learning Schedule : 학습률(learning rate)을 학습이 진행됨에 따라 조정하는 전략
- 학습률 : 모델이 파라미터를 얼마나 빠르게 업데이트할지를 결정하는 중요한 하이퍼파라미터
- Learning Schedule 은 학습률을 동적으로 조정하여 모델의 성능을 최적화; 모델이 빠르게 수렴하면서도, 세밀한 최적화 단계를 통해 더 나은 결과를 얻을 수 O

📙 내일 일정
- 회귀, 차원 축소, 클러스터링

'TIL _Today I Learned > 2024.08' 카테고리의 다른 글
| [DAY 29] Machine Learning 실습 (0) | 2024.08.22 |
|---|---|
| [DAY 28] 회귀 / 차원축소 / 클러스터링 (0) | 2024.08.21 |
| [DAY 26] Machine Learning 개론 (1) | 2024.08.19 |
| [DAY 25] Django 웹 애플리케이션 개발, 웹 크롤링 (0) | 2024.08.14 |
| [DAY 24] Django 웹 애플리케이션 개발 (0) | 2024.08.13 |



